When running a transition state search or geometry optimisation in orca, some of the quantites like forces in cartesian coordinates are only written to the *.opt file that is not mentioned in the manual. Here is a description of the file contents and formats. The file is set up in […]
Blog
This post describes how to run the quantum chemical software package orca on particular clusters. The problem Orca’s parallel implementation relies on a particular OpenMPI version (2.0.2) which is called via a system call to mpirun. Now some clusters do not support mpirun, as they run in SLURM native mode. […]
This article describes how to deploy a Microsoft Azure compute instance to use with a CP2K compiled from scratch.
If you have a MS SQL Server that is reachable in the local network (from remote machines) but it is not accessible if you connect via VPN (you get error 26), then the reason is that the UDP package on port 1434 is not routed by your VPN (which is […]
Hematite (Fe2O3) is a promising transition metal oxide used in a multitude of fields, in particular water splitting. In many of these applications, its interface with water is of crucial importance. However, a computational modeling approach is highly difficult due to the antiferromagnetic ordering and strongly correlated electrons.
Ever wondered how relevant the R^2 value of any data series actually is? Sometimes, you see reasonably good coefficients of determination (depending on your scientific discipline and research question, “reasonably good” means something between .2 and .99) for comparably small data sets. This is not how this works.
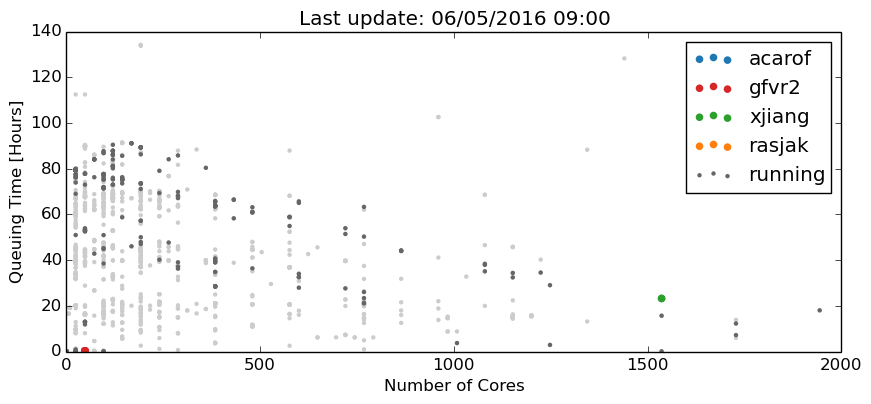
Whenever you run calculations on a large machine (e.g. ARCHER), your jobs are subject to queuing policies. Since the waiting time should be fair (whatever this means), these queueing policies are complex and often consist of several hundred rules. However, from a user perspective, the only interesting question is
Plesk 12.5 (together with the Let’s Encrypt plugin) is a convenient tool that comes with batteries included for most cases. However, webmail is only accessible via SSL with the self-signed certificate by default. Some people suggest patching the config files (which potentially gives problems after updates), but here is a […]
Hematite (Fe2O3) is a promising transition metal oxide used in a multitude of fields, in particular water splitting. In many of these applications, its interface with water is of crucial importance. However, a computational modeling approach is highly difficult due to the antiferromagnetic ordering and strongly correlated electrons. In the […]
DCD files are quite versatile but suffer from nearly non-existing documentation except for some quite dated code that gets copied around between open source projects. They can hold atomic coordinates, velocities and forces – all designated by a different DCD file header: CORD, VEL, FRC. CP2K allows the user to […]
When you are frequently hopping between SSH hosts in different shells, you may forget which nodes you went through to actually get to the host you are on now. With the following changes, you can extend your bash prompt to show any intermediate hosts you went trough:
If you do unrestricted DFT calculations with CP2K for charged systems, you may wonder which spin channel the electron is taken from or added to. Moreover, the sign convention for any output (Hirshfeld or Mulliken spin charge, cube files) may be of interest to you.